Loģisko operāciju veidi

Programmēšana

1. LOĢISKĀ NEGĀCIJA (INVERSIJA)

To veido no vienkārša paziņojuma, predikātam pievienojot partikuli NOT vai izmantojot runas figūru "TĀ NAV TAISNĪBA ...".

	Vērtība	inversija A	Tas nozīmē, ka ne A
Man ir prefikss "DENDY" Iepriekšējā nodaļā mēs uzzinājām, kas ir digitālā informācija. Digitālā informācija tiek attēlota kā biti, kas var iegūt vērtības 1 vai Šajā nodaļā mēs sākam mācīties, kā veikt aprēķinus un veikt citus darbus, izmantojot digitālo informāciju. Lielu daļu no tā, ko mēs apspriedīsim, oficiāli formulēja Džordžs Būls savā rakstā An Enquiry into the Laws of Thought, uz kura balstās šajā grāmatā publicētās loģikas un varbūtību matemātiskās teorijas. Tajā laikā bija maz lietojumprogrammu, taču galu galā zinātnieki un inženieri saprata, ka viņa sistēmu var izmantot efektīvas datorloģikas izveidei. Matemātikas nozare ar digitālo loģiku tiek trāpīgi nosaukta par Būla algebru.		Man nav prefiksa "DENDY"
Es nezinu ķīniešu valodu		Tā nav taisnība, ka es nezinu ķīniešu valodu (es zinu ķīniešu valodu)

Inversiju apzīmē: nav A; ¬A; nevis A

Mūs interesē formas paziņojuma patiesuma vērtība nevis A(nevis tā saturs). To nosaka speciāli patiesības tabula, kas inversijas darbībai izskatās šādi:

Šie trīs operatori veido visu digitālās loģikas pamatu. Faktiski gandrīz visu, ko dara jūsu dators, var aprakstīt ar šīm trim darbībām. Par laimi, šīs darbības nav grūti saprast, jo to nozīme atgādina ikdienas valodā lietoto vārdu nozīmi.

Var aprakstīt ar šādu patiesības tabulu. Dažreiz to norāda ar plus zīmi aplī. Šī ir ļoti noderīga funkcija digitālajā elektronikā, taču tā nav svarīgs jēdziens Būla algebrā. Diemžēl šķiet, ka datorzinātnes, inženierzinātnes un matemātika nespēj panākt vienprātību, tāpēc mēs paliekam pie abiem formātiem. Citām grāmatām, īpaši tām, kas attiecas uz tīru loģiku vai diskrētu matemātiku, var būt dažādi apzīmējumi, tāpēc, ja meklējat citas grāmatas, jums jāzina cits apzīmējums.

Mnemoniskais noteikums: vārds “inversija” (no latīņu valodas inversio — apgriezties) nozīmē, ka baltā krāsa mainās uz melnu, laba par ļaunu, skaista par neglītu, patiesība par melu, meli pret patiesību, nulle pret vienu, viens pret nulli.

1. piezīme. Loģiķi dod priekšroku izteicieniem "tas nav taisnība", jo tas uzsver visa priekšlikuma noliegumu.

Tā kā šī ir inženierzinātņu grāmata, mēs neizmantosim šos apzīmējumus. Būla algebrai, tāpat kā parastajai algebrai, ir noteikti noteikumi. Šie noteikumi ir asociativitātes, sadalījuma, komutācijas un de Morgana likumi. Daži no šiem likumiem var šķist nenozīmīgi, jo jūs esat pie tiem tik ļoti pieraduši. Tomēr, kad tika izveidota Būla algebra ar tās dažādiem noteikumiem, katra aksioma, ko mēs uzskatām par pašsaprotamu normālā algebrā, vairs nebija garantēta. Šie likumi ir pierādīti Būla algebrai.

Asociativitāte ir algebras īpašība, ka terminu novērtēšanas secībai nav nozīmes. Komutativitāte ir īpašība, ka operatora piemērošanas secībai nav nozīmes. Visbiežāk izmantoto operatoru aprakstošs saraksts. Piešķiršanas operatori ir visizplatītākie un ļauj nodot vērtības mainīgajiem. Kartēšana ir process, kurā mēs ievietojam vērtību mainīgajā.

2. piezīme. Divreiz vai četras reizes noliegtam apgalvojumam ir tāda pati patiesības vērtība kā atbilstošajam nenoliedzošajam apgalvojumam trīsreiz noliegts kā vienreiz noliegts.

LOĢISKAIS REIKINĀJUMS (savienojums)

To veido, apvienojot divus apgalvojumus vienā, izmantojot savienību "Un".

P PIEMĒRI: Pieņemsim, ka no mana loga ir redzama stāvvieta, kur parasti ir divas mašīnas: mersedess un žigulis, bet var būt viena vai neviena. Apzīmēsim apgalvojumus:

Mēs jau esam izveidojuši mainīgos un piešķīruši vērtības, tāpēc jums tie ir jāatpazīst. Turklāt piešķīrumā var būt gadījums, kad piešķiramā vērtība ir darbības veikšanas rezultāts. Protams, jūs atņemat vērtību. Pirms izteiksmes piešķiršanas tā tiek saskaitīta un pēc tam tiek piešķirta vērtība.

Kā redzat, piešķiršana ir ļoti vienkārša darbība, kas atrodas operatora labajā pusē, tiek piešķirta mainīgajam kreisajā pusē. Piezīme. Skatiet zemāk "virknes darbības", lai izprastu savienošanu. Mūsu apstākļos tos galvenokārt izmanto, lai salīdzinātu divus mainīgos un pārbaudītu, vai tie atbilst operatora rekvizītam.

Saiklis B un "Žiguli"

Darbība savienojums tiek apzīmēts:Λ; &; *; un; un.

No patiesības tabulas izriet, ka savienojuma darbība ir patiesa tad un tikai tad, ja abi apgalvojumi ir patiesi, un nepatiesa, ja vismaz viens apgalvojums ir nepatiess. Dažreiz šī īpašība tiek sajaukta ar loģiskās reizināšanas darbības definīciju.

Bet visbiežāk tiek izmantoti citi, kurus patiešām ir ļoti viegli iemācīties, lai gan, lai redzētu interesantus piemērus, mums ir jāsaprot kontroles struktūras. Tas ir tāpēc, ka salīdzināšanas darbībā ar operatoru == netiek ņemti vērā mainīgo veidi. Tomēr tagad apskatiet šādu kodu.

Loģiskie operatori tiek izmantoti loģisku darbību veikšanai neatkarīgi no dublēšanas. Tās ir darbības, kas galu galā atgriezīs "jā" vai "nē", pozitīvas vai negatīvas. Tos izmanto kopā ar salīdzināšanas operatoriem, ja to pieprasa nosacījuma izteiksme.

Mnemoniskais noteikums: savienojums ir loģisks reizināšana

Daudzu krustojums

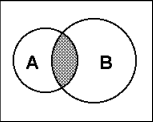
A - daudzi izcilnieki B klasē - daudzi sportisti A  B klasē - daudzi izcilnieki, kas nodarbojas ar sportu

Un loģiskā darbība būs patiesa, ja abi ir patiesi.
Loģiskā darbība "vai" būs patiesa, ja viena no tām ir patiesa.

Loģiskie operatori parasti tiek izmantoti arī izteiksmēs, kuras plānojat novērtēt vadības struktūrās. Tās darbībai parasti ir jēga, ja, strādājot ar Būla vērtībām vai izteiksmēm, kas kādreiz tika novērtētas, tiek iegūtas Būla vērtības.

Iemesls ir tāds, ka katram operatoram ir atšķirīga operatora pieredze. Tie kalpo, lai palielinātu vai samazinātu mainīgā lieluma vērtību par vienu. Tie ir īsceļi uz tipisku darbību cilpas kontūrās, lai palielinātu vai samazinātu vērtību, ko izmantojam, lai sekotu līdzi pabeigtajām iterācijām.

LOĢISKS PAPILDINĀJUMS (ATSAUKŠANA)

To veido, apvienojot divus apgalvojumus vienā, izmantojot savienību VAI.

Piemēri

Rīt līs vai nē (trešo nedod).

Petja sēž uz stadiona rietumu vai austrumu tribīnēm.

Students brauc vilcienā vai lasa grāmatu.

Norādīts:

Šie operatori ir interesanti, jo tie veic divas lietas, tāpat kā kombinētie piešķiršanas operatori, ko redzējām iepriekš. No vienas puses, samazinās vai palielinās, un, no otras puses, tie tiek atgriezti operatora rezultātā. Lai pabeigtu izpratni, labāk ir izpētīt šo kodu.

Šajā kodā mēs iegūstam dažādas lietas kā izvadi ar priekšpieaugumu un pēcpieaugumu. Komentārā tiks parādīts šāds rezultāts. Analizējiet to un sapratīsit, kā tas ir iespējams. Strādājot ar virknēm, mums ir īpašs operators, kas ir savienošana. Tas kalpo vienas ķēdes pievienošanai otrai.

A vai B; A VAI B; A | AT; A V B

PIEMĒRI: Teiksim, no mana loga ir redzama stāvvieta, kur parasti ir divas mašīnas: mersedess un žigulis, bet var būt viens, vai arī neviena. Apzīmēsim apgalvojumus:

A = Stāvvietā ir Mercedes

B = Stāvlaukumā novietots žigulis

Disjunkcija B = Stāvlaukumā ir Mercedesvai "Žiguli"

Apgūstot programmēšanas valodu, īpaša uzmanība jāpievērš operatora prekursoram, kas būtībā ir noteikumu kopums un kārtība, pēc kuras operatori tiks novērtēti, strādājot ar izteiksmēm, kas ietver vairākas no tām.

Tāpat kā matemātikā, dažreiz, ja mēs veicam darbības vienā vai otrā secībā, arī galīgās vērtības var mainīties. Programmēšanas valodās atkarībā no šo operatoru lietošanas secības izteiksmes var radīt dažādus rezultātus.

Operatora prioritāte palīdz noskaidrot šīs šaubas un to, ka programmētāji a priori zina, kā valoda atrisinās izteiksmes, spējot tās uzrakstīt tā, lai risinājums būtu tāds, kādu viņi gaidīja. Tomēr valodas prognoze ne vienmēr ir tā, ko mēs vēlamies izmantot. Lai padarītu lietas vieglāku, ir iekavas, kas ļauj mums definēt mūsu izteicienus, norādot, kuri apgalvojumi ir jāatrisina vispirms. Citiem vārdiem sakot, ikreiz, kad mēs izmantojam iekavas, mēs piespiežam kompilatoru atrisināt noteiktas darbības pirms tam, neskatoties uz tā iestatīto noklusējuma prioritāti.

No patiesības tabulas izriet, ka disjunkcijas darbība ir nepatiesa tad un tikai tad, ja abi apgalvojumi ir nepatiesi, un patiesa, ja vismaz viens apgalvojums ir patiess. Dažreiz šī īpašība tiek sajaukta ar loģiskās reizināšanas darbības definīciju.

Mnemoniskais likums: disjunkcija ir loģiska papildinājums un mums nav šaubu, ka esat pamanījis:

Iepriekš rakstītais izteiciens: 10 nederēs dažādām interpretācijām. Pretējā gadījumā mums vienmēr ir jāizmanto iekavas, radot sarežģītības izteiksmes, kas ir lielākas nekā nepieciešams. Iespējams arī, ka, lai gan mēs labi zinām priekšgājēju, iekavu izvietošana var palīdzēt koda lasāmībai, jo ikviens lasītājs, kurš redz iekavas, uzreiz zinās, ka šī izteiksmes daļa tiks novērtēta agrāk. Šīs četras darbības būs mikro, un katra no tām atbildīs divu ciparu binārai kombinācijai.

bet loģikā: 1 V 1 = 1.

Komplektu savienība

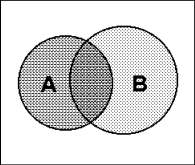
A - izcilnieku komplekts B klasē - sportistu komplekts A klasē  B - klases skolēnu kopums, kuri ir teicamnieki vai sportisti

LOĢISKĀ SEKOŠANA (IETEKME)

Pieņemsim, ka mēs vēlamies veikt divu zīmju skaitļu reizināšanu kā -2 un -4. Apskatīsim mūsu gadījumu, kas parādīts iepriekšējā tabulā. Otrajā rindā varat redzēt katra mūsu uzdevumā mainīgā lieluma iniciāļus. 3. rindā var novērot šīs nobīdes rezultātu, kas ir vienāds ar loģisko nobīdi, jo tikai pirmajā daļā redzējām, ka zīmes bits vienmēr tiek saglabāts. Salīdzinot trešo rindu, kas ir pirmā cikla rezultāts, var redzēt, ka biti ir vienādi, tāpēc otrā cikla laikā notiks tikai aritmētiskā nobīde.

To veido, apvienojot divus apgalvojumus vienā, izmantojot runas figūru "JA ..., TAD ..."

PIEMĒRI

Ja tiek dots zvērests, tad tas ir jāpilda.

Ja skaitlis dalās ar 9, tad tas dalās ar 3.

Vēsturiski implikācijas darbība tika ieviesta, lai pabeigtu divu mainīgo loģisko funkciju sistēmu, tāpēc loģikā ir pieļaujams (pieņemts, saskaņots) aplūkot no ikdienas viedokļa bezjēdzīgus apgalvojumus. Sniegsim piemērus, kurus ir ne tikai pamatoti ņemt vērā loģikā, bet arī to nozīme ir patiesa.

4. rindā parādīts šīs maiņas rezultāts. Šīs darbības rezultātu var novērot virknē. Pēc katras operācijas ir nepieciešams veikt rezultāta nobīdi. 6. rindā parādīts šīs nobīdes rezultāts. Šī 6. rinda ir trešā cikla beigas. Salīdzinot 6 bitus rindā, mēs redzam, ka tie ir vienādi, tāpēc mums ir jāveic tikai aritmētiskā nobīde ceturtajā ciklā. Rezultāts tiek parādīts rindā. Tā kā skaitļiem ar 4 bitiem ir nepieciešami tikai 4 cikli. Šajā nodaļā mēs analizēsim mūsu izstrādātā procesora atmiņas funkciju.

Datorā katra programma, kuru mēs palaižam, tiek saglabāta galvenajā atmiņā, kas ir tipa atmiņa. Mikroprocesors ņem no atmiņas instrukcijas un datus, kas tam nepieciešami nejaušā secībā atbilstoši programmai vai kurus tie tajā brīdī izpilda. Tādā pašā veidā mūsu mikroprocesoram būs atmiņa, kurā tiks saglabāti dati un instrukcijas, kuras mēs vēlamies saglabāt.

Ja govis lido, tad 2 + 2 = 5

Ja es esmu Napoleons, tad kaķim ir četras kājas.

Ietekme tiek apzīmēta: A B;

Viņi saka: "Ja A, tad B", "A nozīmē B", "A nozīmē B", "B izriet no A".

No patiesības tabulas var redzēt, ka divu apgalvojumu implikācija ir nepatiesa tad un tikai tad, ja no patiesa apgalvojuma izriet nepatiess apgalvojums (patiesa premisa noved pie nepatiesa secinājuma). Dažreiz šis īpašums tiek pieņemts definīcija implikācijas operācijas.

Ideja ir tāda, ka jūs varat saglabāt informāciju tajos un nezaudēt šo informāciju gadu gaitā vai integrācijas samazināšanas laikā. Iepriekš kāds no pakalpojumu sniedzēja iesniedza specifikāciju saturam, kuru viņi vēlējās. Tas bija saistīts ar faktu, ka zibakcijā ietvertā informācija tika iestatīta ražošanā. Tomēr tas bija šķērslis tiem, kuriem bija vajadzīga atmiņa, lai izveidotu mazu, un viņiem nebija pietiekami daudz, lai pieprasītu atmiņu izplatītājiem, izņemot to, ka izplatītāji veica tikai lielus pasūtījumus.

LOĢISKĀ VIENLĪDZĪBA (EKVIVALENCE)

To veido, apvienojot divus apgalvojumus vienā, izmantojot runas figūru "... TAD UN TIKAI TAD, KAD ...".

PIEMĒRI

“Leņķi sauc par taisnu leņķi tad un tikai tad, ja tas ir 90 grādi.

“Divas taisnes ir paralēlas tad un tikai tad, ja tās nekrustojas.

Šādu atmiņu var ierakstīt elektriski un izdzēst ar ultravioleto gaismu. Tiem, kam nebija UV gaismas moduļa, vajadzēja "paņemt saulītē" savas atmiņas, kurām bija tāds kā "logs", pa kuru iekļuva UV gaisma. UV ģeneratora gadījumā programmētājiem vajadzēja ne vairāk kā 8 minūtes, lai izdzēstu atmiņu, bet tiem, kam šīs iespējas nebija, atmiņas jāatstāj saulē uz aptuveni 24 stundām. Turklāt šīs atmiņas varētu pierakstīt un izdzēst apmēram 10 reizes.

“Jebkurš materiālais punkts saglabā miera stāvokli vai vienmērīgu taisnvirziena kustību tad un tikai tad, ja ārēja darbība šo stāvokli nemaina” (Ņūtona pirmais likums).

“Galva domā tad un tikai tad, kad mēle ir mierā” (Joks)

Visi matemātikas, fizikas likumi, visas definīcijas ir priekšlikumu ekvivalence.

Šo procesu var veikt tūkstoš reižu, un tas prasīja tikai dažas minūtes. Šāda veida atmiņu var izdzēst un ierakstīt tik reižu, cik nepieciešams. Vienīgais trūkums ir tas, ka tajā ierakstīto informāciju var izmantot tikai tad, ja tā ir derīga. Kad barošana ir izslēgta, ierakstītie dati tiks nekavējoties dzēsti. Tie tiek izmantoti tikai kā pagaidu uzglabāšana.

Uzlādes esamība vai neesamība kondensatorā tiek interpretēta kā 1 vai 0 binārs. Pieņemsim, ka mums ir grāmatu tirgotājs ar 4 rindām. Katrā rindā var ievietot līdz 4 grāmatām.

Atmiņas kā grāmatu tirgotāja reprezentācija. Līnijas apzīmē šīs atmiņas adreses vai vietas, kas pieejamas informācijas glabāšanai. Katrs no tiem atspoguļo mazliet informācijas, tāpēc mūsu grāmatu tirgotājs ir atmiņa ar četrām adresēm ar četru bitu ietilpību. Katrs no tiem ir parādīts secīgi binārais skaitlis.

Ekvivalence ir apzīmēta: A = B; A~B

PIEMĒRS. Ļaujiet dot divus teikumus:

A \u003d “Cipars dalās ar 3 bez atlikuma (trīs reizinājums)”

B = "Cipara ciparu summa dalās ar 3".

BETlīdzvērtīgs B = "Cipars dalās ar 3 bez atlikuma tad un tikai tad, ja dotā skaitļa ciparu summa dalās ar 3."

No patiesības tabulas izriet, ka divu apgalvojumu līdzvērtība ir patiesa tad un tikai tad, ja abi šie apgalvojumi ir patiesi vai abi ir nepatiesi. Dažreiz šis īpašums tiek pieņemts kā definīcija ekvivalences operācijas.

Loģiskās funkcijas

loģika kā zinātne;

propozīcijas algebra;

loģiskās operācijas;

loģiskās funkcijas;

mājasdarbs.

Loģiskās algebras formulas izmanto tikai Būla mainīgos. Loģiskie savienojumi (UN, VAI) apzīmē loģiskās darbības. Katra formula definē loģisko funkciju, kas pati par sevi var ņemt tikai vienu no divām loģiskajām vērtībām (0 vai 1). Tas ir, izteiksmes E \u003d A V B vietā varat rakstīt F (A, B) \u003d A V B un uzskatīt to par divu mainīgo funkciju.

Mēs esam apskatījuši divu mainīgo loģiskās pamatoperācijas. Cik dažādu loģisko (t.i., divu mainīgo) funkciju var būt diviem mainīgajiem? Mēģināsim atbildēt uz šo jautājumu.

Divi mainīgie, no kuriem katrs var būt nulle vai viens, veido 2 2 = 4 dažādas vērtību kopas: (0,0); (0,1); (1,0); (1.1). Katrai kopai pašai funkcijai var būt vērtība 0 vai 1. Piemēram, F(0,0)=1; F(0,1)=1; F(1,0)=0; F(1,1)=0. Tad būs sešpadsmit dažādas divu mainīgo funkcijas (4 2 =16).

Tabulā parādīts, ka katra funkcija atbilst tās noliegumam (konstante 1 - konstantes 0 noliegums).

Funkciju var norādīt gan formulas, gan tabulas veidā. Pāreja no tabulas uzdevuma uz Būla formulu vienmēr ir iespējama.

Divu mainīgo loģisko funkciju kopsavilkuma tabula

X vērtība
Y vērtība
	Funkcijas vērtība	Funkcijas nosaukums	Funkciju apzīmējums
Funkcija 0		konstante 0
1. funkcija		savienojums
2. funkcija		implikācijas XY noliegums	F=  (X  Y)
3. funkcija		mainīgais X
4. funkcija		implikācijas YX noliegums	F= (Y  X)
5. funkcija		mainīgais Y
6. funkcija		ekvivalences noliegums	F=  (X  Y)
7. funkcija		disjunkcija
8. funkcija		disjunkcijas noliegums
9. funkcija		līdzvērtība
10. funkcija		noliegums Y
11. funkcija		implikācija YX
12. funkcija		noliegums X
13. funkcija		implikācija XY
14. funkcija		savienojuma noliegums	F =  (X  Y)
15. funkcija		konstante 1

KOMPLEKSS PAZIŅOJUMS

Ja vairākus vienkāršus apgalvojumus apvieno vienā, izmantojot loģiskās darbības, tad šādu paziņojumu sauc par sarežģītu.

Mēs vienmēr izejam no tā, ka jebkuramvienkārši definēti apgalvojumi (zināms ), vai tā ir patiesa vai nepatiesa. Autorskomplekss apgalvojumus un saskaņā ar tajā ietverto loģisko darbību patiesuma tabulām vienmērvar definēt vai tā ir patiesība vai nepatiesa.

Kā likums, mēs saņemam reālu uzdevumu dabiskās valodas teksta veidā. Un pirms turpināt tās risinājumu, mums ir jāizceļ vienkārši apgalvojumi, attiecības (savienojumi) starp tiem un jāpārtulko formulu valodā (formalizē problēmas stāvokli, nosaka formu). Apskatīsim sarežģītu apgalvojumu formalizācijas piemērus.

Nosakiet kompleksa paziņojuma formu

1. piemērs. E = "Jūsu ierašanās nav ne nepieciešama, ne vēlama" Saliktie apgalvojumi: A = "Jūsu ierašanās ir nepieciešama"; B = "Jūsu apmeklējums ir laipni gaidīts"

Atbilde: E = nav (A) un nav (B)

Piemērs 2. E \u003d "Ienaidnieka meklēšana ilga trīs stundas, bet nebija rezultātu, slēpošais ienaidnieks nepadevās" Saliktie paziņojumi: A \u003d "Ienaidnieka meklēšana ilga trīs stundas" B \ u003d "Ienaidnieks tika atrasts (ir rezultāts)" C \u003d " Ienaidnieks ir sevi nodevis." Atbilde: E= nav(C) → A & nav(B)

Piemērs 3. E = "Ja vakar bija apmācies, tad šodien spoži spīd saule" A = "Vakar bija apmācies"; B = "Šodien spoži spīd saule"

Atbilde: E = A → B

LOĢISKĀS DARBĪBAS PRIORITĀTE

loģika kā zinātne;

propozīcijas algebra;

loģiskās operācijas;

loģiskās funkcijas;

loģisko operāciju prioritāte;

identiski patiesas un identiski nepatiesas darbības;

loģikas algebras pamatlikumi;

loģisko likumu pierādījums;

vienkāršākie informācijas pārveidotāji;

mājasdarbs.

Loģisko izteiksmju vērtību novērtējums tiek veikts noteiktā secībā atbilstoši to prioritātei:

- inversija

- savienojums

- disjunkcija

- implikācija un līdzvērtība

Tās pašas prioritātes darbības tiek izpildītas no kreisās puses uz labo. Priekš pārkārtošana tiek izmantotas darbības iekavās.

1. PIEMĒRS: A V (B→ C) un D = nav (A)

Izpildes kārtība:

Nav (A) - inversija

AT → C - implikācija

(AT → C) & D - savienojums

A V (B → C) & D - disjunkcija

A V (B → C) & D = nav(A)-ekvivalence

Izveidosim apgalvojuma patiesības tabulu

E = (A V nav(B)) → nav(C)

Apgalvojums E ietver trīs mainīgos: A, B, C (n=3) un četras loģiskās operācijas: inversija B, inversija C, disjunkcija, implikācija.

Patiesības tabulā būs 2 3 + 2 (galvene) = 8 +2 = 10 rindas un 3 + 4 = 7 kolonnas


						A v nav(B) → nav(C)

IDENTISKI PATIESI UN IDENTISKI MELTĪGI APSTIPRINĀJUMI

loģika kā zinātne;

propozīcijas algebra;

loģiskās operācijas;

loģiskās funkcijas;

loģisko operāciju prioritāte;

identiski patiesas un identiski nepatiesas darbības;

loģikas algebras pamatlikumi;

loģisko likumu pierādījums;

vienkāršākie informācijas pārveidotāji;

mājasdarbs.

Ja komplekss apgalvojums ir patiess visām tajā iekļauto mainīgo vērtībām, tad šādu apgalvojumu sauc par IDENTISKI TRUE vai tautoloģiju (apzīmē ar konstanti 1).

PIEMĒRAM paziņojums: "Demokrāts ir cilvēks, kurš apliecina demokrātiskus uzskatus" vienmēr ir taisnība, tas ir, tā ir tautoloģija.

Visi matemātiskie, fiziskie un citi likumi ir tautoloģijas. Piemēram: (a+b) 2 = a 2 + 2ab + b 2

Laika prognoze rītdienai varētu būt, piemēram: "Līs vai nelīs."Šāds pareģojums vienmēr būs patiess, lai gan diez vai tas kādam derēs. Viņa matemātiskais apzīmējums:

A V nav (A) \u003d 1

(saskaņā ar izslēgtā vidus likumu vai nu spriedumam, vai tā noliegumam vienmēr jābūt patiesam).

Izmantojot patiesības tabulu, varat pārbaudīt, vai sarežģīts apgalvojums ir identiski patiess.

Ja salikts apgalvojums ir nepatiess visām tajā iekļauto mainīgo vērtībām, tad šādu paziņojumu sauc par IDENTISKI FALSE (apzīmē ar konstanti 0).

PIEMĒRAM, apgalvojums: "Šodien ir trešdiena, un šī ir nedēļas otrā diena" ir identiski nepatiess. Šis apgalvojums ir identiski nepatiess: "Dators ir ieslēgts un dators nav ieslēgts (izslēgts)". Tā matemātiskais apzīmējums ir šāds:

A un ne(A) = 0

(Saskaņā ar pretrunu likumu: apgalvojums un tā noliegums nevar būt patiesi vienlaikus.)

Ja sarežģītu paziņojumu vērtības ir vienādas visām iespējamajām tajos iekļauto mainīgo vērtībām, tad šādus paziņojumus sauc par EVIVALENTIE, IDENTISKI, EVIVALENTI

Vienkāršošana ir sarežģīti apgalvojumi nomaiņa paziņojumi līdz ekvivalentam viņam, pamatojoties uz propozicionālās algebras likumiem

LOĢIKAS ALGEBRAS PAMATLIKUMS (EKVIVALENCES).

loģika kā zinātne;

propozīcijas algebra;

loģiskās operācijas;

loģiskās funkcijas;

loģisko operāciju prioritāte;

identiski patiesas un identiski nepatiesas darbības;

loģikas algebras pamatlikumi;

loģisko likumu pierādījums;

vienkāršākie informācijas pārveidotāji;

mājasdarbs.

Risinot loģiskās problēmas, bieži vien ir jāvienkāršo formulas. Formulu vienkāršošana Būla algebrā balstās uz līdzvērtīgām transformācijām, kuru pamatā ir pamatlikumi.

Propozicionālās loģikas likumi ir tādas izteiksmes, kurām vienmēr atbilst patiess priekšlikums neatkarīgi no tā, kādu vērtību aizstāšanu mēs veicam mainīgo vietā. Propozīcijas algebrā loģiskie likumi tiek izteikti kā formulas.

1.1. Identitātes likums:

Katra doma ir identiska pati ar sevi, tas ir, "A ir A", kur A ir jebkurš apgalvojums.