Видове логически операции
1. ЛОГИЧЕСКО ОТРИЧАНИЕ (ИНВЕРЦИЯ)
Образува се от просто твърдение чрез добавяне на частицата НЕ към сказуемото или чрез използване на фигурата на речта „НЕ Е ВЯРНО, ЧЕ...“.
|
Стойност А |
инверсия А |
Стойността не е A |
|
|
Имам префикса "DENDY" В предишната глава научихме какво е цифрова информация. Цифровата информация е представена като битове, които могат да приемат стойностите 1 или В тази глава започваме да се учим как да извършваме изчисления и друга работа, използвайки цифрова информация. Голяма част от това, което ще обсъдим, е формализирано от Джордж Бул в неговата статия „Изследване на законите на мисълта“, на която се основават математическите теории на логиката и вероятността, публикувани в тази книга. По това време имаше малко приложения, но в крайна сметка учени и инженери осъзнаха, че неговата система може да се използва за създаване на ефективна компютърна логика. Клонът на математиката с цифрова логика е подходящо наречен Булева алгебра. |
Нямам префикс "DENDY" | ||
|
Не знам китайски език |
Не е вярно, че не знам китайски (знам китайски) |
Инверсията е обозначена: не A; ¬A; не А
Ние се интересуваме от стойността на истината на изявление на формата не А(а не съдържанието му). Определя се от специални таблица на истината, което за операцията на инверсия изглежда така:
Тези три оператора формират основата на всичко в цифровата логика. Всъщност почти всичко, което компютърът ви прави, може да се опише чрез тези три операции. За щастие тези операции не са трудни за разбиране, тъй като техните значения наподобяват значенията на думите, използвани в ежедневния език.
Може да се опише със следната таблица на истината. Това понякога се обозначава със знак плюс в кръг. Това е много полезна функция в цифровата електроника, но не е важна концепция в булевата алгебра. За съжаление компютърните науки, инженерството и математиката изглежда не могат да постигнат консенсус, така че се придържаме към двата формата. Други книги, и особено тези, занимаващи се с чиста логика или дискретна математика, може да имат различна нотация, така че ако се правят справки с други книги, е необходимо да се знае различната нотация.
Мнемонично правило:думата "инверсия" (от латинското inversio - обръщане) означава, че бялото се променя в черно, доброто в зло, красивото в грозно, истината в лъжа, лъжа в истина, нула в едно, едно в нула.
Бележка 1.Логиците предпочитат да боравят с изразите „това не е вярно“, тъй като това подчертава отрицанието на цялото твърдение.
Тъй като това е инженерна книга, ние няма да използваме тези обозначения. Булевата алгебра, подобно на обикновената алгебра, има определени правила. Тези правила са законите на асоциативността, разпределението, комутацията и Де Морган. Някои от тези закони може да изглеждат тривиални, защото сте свикнали с тях. Въпреки това, когато булевата алгебра беше създадена с нейните различни правила, всяка аксиома, която приемаме за даденост в нормалната алгебра, вече не беше гарантирана. Тези закони са доказани за булевата алгебра.
Асоциативността е свойство на алгебрата, че редът на оценяване на термините е без значение. Комутативността е свойството, че редът, в който се прилага даден оператор, е несъществен. Описателен списък на най-често използваните оператори. Операторите за присвояване са най-често срещаните и ви позволяват да предавате стойности на променливи. Картографирането е процесът, чрез който поставяме стойност в променлива.
Бележка 2.Твърдение, отречено два пъти или четири пъти, има същата истинност като съответното неотречено твърдение, а твърдение, отречено три пъти, има същата истинност като твърдение, отречено веднъж.
ЛОГИЧЕСКО УМНОЖЕНИЕ (СЪЕДИНЕНИЕ)
Образува се чрез комбиниране на две твърдения в едно с помощта на връзката „I“.
ППРИМЕРИ: Да кажем, че от прозореца си виждам паркинг, където обикновено има две коли: мерцедес и жигули, но може да има една от тях или да няма нито една. Нека означим твърденията:
Вече създадохме променливи и присвоихме стойности по-рано, така че трябва да ги разпознаете. Освен това при присвояване може да има случай, при който стойността, която трябва да бъде присвоена, е резултат от операция. Разбира се, изваждате стойността. Преди присвояването изразът се брои и след това му се присвоява стойност.
Както можете да видите, присвояването е много проста операция, това, което е отдясно на оператора, се присвоява на променливата отляво. Забележка. Погледнете по-долу „операции с низове“, за да разберете конкатенацията. Те се използват главно в нашата среда за сравняване на две променливи и проверка дали съвпада със свойство на оператор.
Съюз Б И "Жигули"
Операция връзката се обозначава с:Λ; &; *; и; И.
От таблицата на истината следва, че операцията конюнкция е вярна тогава и само ако и двете твърдения са верни, и невярна, когато поне едно твърдение е невярно. Понякога това свойство се приема като дефиниция на операцията за логическо умножение.
Но тези, които се използват най-много, са други, които наистина са много лесни за научаване, въпреки че за да видим интересни примери, трябва да разберем контролните структури. Това е така, защото операцията за сравнение, извършена с оператора ==, не взема предвид типовете променливи. Сега обаче вижте следния код.
Логическите оператори се използват за извършване на логически операции, независимо от излишъка. Това са операции, които в крайна сметка ще върнат „да“ или „не“, положително или отрицателно. Те се използват в комбинация с оператори за сравнение, когато се изискват от израз на условие.
Мнемонично правило:връзката е логична умножение
Пресечна точка на много
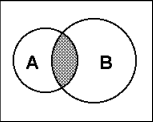
A - много отлични ученици в клас B - много спортисти в клас A B - много отлични ученици, занимаващи се със спорт
- И една логическа операция ще бъде вярна, ако и двете са верни.
- Логическият оператор "или" ще бъде верен, ако един от тях е верен.
Причината е, че всеки оператор има различен операторски опит. Те служат за увеличаване или намаляване на стойността на променлива с единица. Те са преки пътища за типична операция в пътища на цикъл за увеличаване или намаляване на стойност, която използваме, за да следим извършените повторения.
ЛОГИЧЕСКО ДОБАВЯНЕ (РАЗДЕЛЯНЕ)
Образува се чрез комбиниране на две твърдения в едно с помощта на връзката ИЛИ.
Примери
Утре ще вали или не (няма трети вариант).
Петя е седнала на западната или източната трибуна на стадиона.
Ученик пътува във влак или чете книга.
Посочва се от:
Тези оператори са интересни, защото правят две неща, точно като комбинираните оператори за присвояване, които видяхме по-рано. От една страна намаляват или увеличават, а от друга страна се връщат в резултат на оператора. За да завършите разбирането, е по-добре да проучите този код.
В този код получаваме различни неща като изход чрез предварително и след нарастване. Следният резултат ще се появи в коментара. Анализирайте го и ще разберете как е възможно това. Когато работим с низове, имаме специален оператор, който е конкатенация. Служи за закрепване на една верига към друга.
А или Б; А ИЛИ Б; A | IN; A V B
ПРИМЕРИ: Да кажем, че от прозореца си виждам паркинг, където обикновено има две коли: мерцедес и жигули, но може да има една от тях, а може и да няма. Нека означим твърденията:
A = На паркинга има Mercedes.
B = На паркинга има автомобили Жигули.
Дизюнкция Б = На паркинга има коли Mercedesили "Жигули"
Когато изучаваме език за програмиране, трябва да обърнем специално внимание на предшественика на оператора, който всъщност е набор от правила и ред, по който операторите ще бъдат оценявани, когато се работи с изрази, включващи повече от един от тях.
Точно както в математиката, понякога, ако извършваме операции в определен ред, крайните стойности също могат да имат промени. В езиците за програмиране, в зависимост от реда, в който се прилагат тези оператори, изразите могат да дадат различни резултати.
Приоритетът на операторите служи за изясняване на това съмнение и че програмистите знаят предварително как езикът ще решава изрази, като могат да ги напишат така, че решението да е това, което са очаквали. Предсказаният език обаче не винаги е този, който искаме да приложим. За да направим нещата по-лесни, има скоби, които ни позволяват да дефинираме нашите изрази, като посочваме кои изрази трябва да бъдат разрешени първи. С други думи, когато използваме скоби, ние принуждаваме компилатора да разреши определени операции преди тях, въпреки приоритета, който е определил по подразбиране.
От таблицата на истината следва, че операцията на дизюнкция е невярна тогава и само ако и двете твърдения са неверни и вярна, когато поне едно твърдение е вярно. Понякога това свойство се приема като дефиниция на операцията за логическо умножение.
Мнемонично правило: дизюнкция е логична допълнение и не се съмняваме, че сте забелязали:
Изразът, написан по-рано по следния начин: 10 няма да се приложи за различни интерпретации. В противен случай от нас се изисква винаги да използваме скоби, създавайки изрази на сложност, които са по-големи от необходимото. Възможно е също така, че въпреки че познаваме добре предшественика, поставянето на скоби може да помогне за четливостта на кода, тъй като всеки читател, който види скобите, веднага ще разбере, че тази част от израза ще бъде оценена първа. Тези четири действия ще бъдат микро и всяко от тях ще съответства на двоична комбинация от две цифри.
но в логиката: 1 V 1 = 1.
Обединение на комплекти
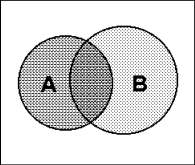
A - много отлични ученици в клас B - много спортисти в клас A B - много ученици в класа, които са отлични ученици или спортисти
ЛОГИЧЕСКО СЛЕДСТВИЕ (ЗНАЧЕНИЕ)
Да кажем, че искаме да извършим умножение на две числа със знак като -2 и -4. Нека разгледаме нашия случай, представен в таблицата по-горе. На втория ред можете да видите инициалите на всяка от променливите в нашето упражнение. В ред 3 можем да наблюдаваме резултата от това отместване. То е равно на логическото отместване, тъй като видяхме само в първата част, че знаковият бит винаги се запазва. Когато сравнявате ред три, който е резултат от първия цикъл, можете да видите, че битовете са еднакви, така че само аритметично изместване ще настъпи по време на втория цикъл.
Образува се чрез комбиниране на две твърдения в едно с помощта на фигурата на речта „АКО..., ТОГАВА...“
ПРИМЕРИ
Щом е дадена клетва, значи трябва да се изпълни.
Ако едно число се дели на 9, то се дели на 3.
Исторически операцията на импликация е въведена, за да завърши системата от логически функции на две променливи, следователно в логиката е допустимо (прието, съгласувано) да се разглеждат твърдения, които са безсмислени от ежедневна гледна точка. Нека дадем примери, които не само са законни за разглеждане в логиката, но в същото време значението им е вярно.
Ред 4 показва резултата от тази промяна. Резултатът от тази операция може да се наблюдава в линията. След всяка операция е необходимо да се компенсира резултатът. Ред 6 показва резултата от това изместване. Този ред 6 е краят на третия цикъл. Сравнявайки битовете в ред 6, виждаме, че те са еднакви, така че просто трябва да извършим аритметично преместване в четвъртия цикъл. Резултатът се показва в реда. Тъй като числата с 4 бита са необходими само 4 цикъла. В тази глава ще анализираме функцията на паметта в процесора, който ще проектираме.
В компютъра всяка програма, която изпълняваме, се съхранява в основната памет, която е вид памет. Микропроцесорът взема от паметта инструкциите и данните, които са му необходими в произволен ред според програмата или която изпълнява в този момент. По същия начин нашият микропроцесор ще има памет, която ще съхранява данните и инструкциите, които искаме да съхраним.
Ако кравите летят, тогава 2 + 2 = 5
Ако аз съм Наполеон, тогава котката има четири крака.
Импликацията се означава: A B;
Те казват: „Ако A, то B“, „A предполага B“, „A влече B“, „B следва от A“.
Таблицата на истината показва, че импликацията на две твърдения е невярна тогава и само ако невярно твърдение следва от вярно твърдение (вярна предпоставка води до невярно заключение). Понякога това свойство се приема за определениеоперации на импликация.
Идеята е, че можете да съхранявате информация в тях и да не губите тази информация през годините или когато намалите интеграцията. Беше така, че някой ще представи спецификация за съдържанието, което иска от доставчика. Това се дължи на факта, че информацията, съдържаща се в спомените, е установена в производството. Това обаче беше пречка за тези, които се нуждаеха от памет, за да разработят малка и нямаха достатъчно, за да поискат от дистрибуторите памет, освен че дистрибуторите правеха само големи поръчки.
ЛОГИЧЕСКО РАВЕНСТВО (ЕКВИВАЛЕНТНОСТ)
Образува се чрез комбиниране на две твърдения в едно с помощта на фигурата на речта „... ТОГАВА И САМО ТОГАВА, КОГАТО...“.
ПРИМЕРИ
“Ъгъл се нарича прав тогава и само ако е равен на 90 градуса.
“Две прави са успоредни тогава и само ако не се пресичат.”
Такава памет може да бъде записана електрически и изтрита от ултравиолетова светлина. За тези, които нямаха модул за ултравиолетова светлина, беше необходимо да „изнесат на слънце“ спомените си, които имаха своеобразен „прозорец“, през който ултравиолетовата светлина проникваше. Ако е оборудван с генератор на ултравиолетова светлина, на програмистите са били необходими не повече от 8 минути, за да изтрият паметта, но тези, които не разполагат с това съоръжение, трябва да оставят спомените си на слънце за приблизително 24 часа. Освен това тези спомени могат да бъдат записани и изтрити приблизително 10 пъти.
“Всяка материална точка поддържа състояние на покой или равномерно праволинейно движение тогава и само ако външно влияние не променя това състояние” (Първият закон на Нютон).
“Главата мисли тогава и само тогава, когато езикът си почива” (Виц)
Всички закони на математиката, физиката, всички дефиниции са същността на еквивалентността на твърденията.
Можете да направите този процес хиляди пъти и отне само няколко минути. Този тип памет може да се изтрива и записва толкова пъти, колкото е необходимо. Единственият недостатък е, че информацията, записана в него, може да се използва само когато е валидна. След като захранването бъде изключено, записаните данни ще бъдат изтрити незабавно. Те се използват само като временно хранилище.
Наличието или липсата на заряд в кондензатора се интерпретира като двоично 1 или 0. Да кажем, че имаме книжар с 4 реда. Всеки ред може да побере до 4 книги. 
Представяне на паметта като книжар. Линиите представляват адресите, които има тази памет, или наличните пространства за съхраняване на информация. Всеки от тях представлява малко информация, така че нашият книжарник е памет с четири адреса с капацитет от четири бита. Всеки от тях е представен последователно двоично число.
Посочена е еквивалентност: A = B; А ~ Б
ПРИМЕР. Нека бъдат дадени две твърдения:
A = „Числото се дели на 3 без остатък (кратно на три)“
B = „Сумата от цифрите на едно число се дели на 3.“
Аеквивалентен B = "Число се дели на 3 без остатък тогава и само ако сборът от цифрите на даденото число се дели на 3."
От таблицата на истината следва, че еквивалентността на две твърдения е вярна тогава и само ако и двете от тези твърдения са верни или и двете са неверни. Понякога това свойство се приема за определениеоперации за еквивалентност.
Логически функции
логиката като наука;
пропозиционална алгебра;
логически операции;
логически функции;
домашна работа.
Формулите на логическата алгебра използват само логически променливи. Логическите връзки (И, ИЛИ) означават логически операции. Всяка формула определя логическа функция, която сама по себе си може да приема само една от две логически стойности (0 или 1). Тоест, вместо израза E = A V B, можете да напишете F(A,B) = A V B и да го разглеждате като функция на две променливи.
Разгледахме основните логически операции на две променливи. Колко различни логически (т.е. двузначни) функции на две променливи може да има? Нека се опитаме да отговорим на този въпрос.
Две променливи, всяка от които може да бъде нула или единица, образуват 2 2 = 4 различни набора от стойности: (0,0); (0,1); (1,0); (1.1). За всеки набор самата функция може да приеме стойност 0 или 1. Например F(0,0)=1; F(0,1)=1; F(1,0)=0; F(1,1)=0. Тогава ще има общо шестнадесет различни функции на две променливи (4 2 =16).
Таблицата показва, че всяка функция съответства на своето отрицание (константа 1 - отрицание на константа 0).
Функцията може да бъде зададена като формула или в таблична форма. Преходът от таблична задача към булева формула винаги е възможен.
Обобщена таблица на логически функции на две променливи
|
X стойност | ||||||
|
Y стойност | ||||||
|
Функционална стойност |
Име на функцията |
Обозначение на функцията |
||||
|
Функция 0 |
константа 0 | |||||
|
Функция 1 |
съчетание | |||||
|
Функция 2 |
отрицание на импликацията XY |
F= (X Y) |
||||
|
Функция 3 |
променлива X | |||||
|
Функция 4 |
отрицание на импликацията YX |
F= (Y X) |
||||
|
Функция 5 |
променлива Y | |||||
|
Функция 6 |
отрицание на еквивалентността |
F= (X Y) |
||||
|
Функция 7 |
дизюнкция | |||||
|
Функция 8 |
отрицание на дизюнкция | |||||
|
Функция 9 |
еквивалентност | |||||
|
Функция 10 |
отрицание на Y | |||||
|
Функция 11 |
импликация YX | |||||
|
Функция 12 |
отрицание X | |||||
|
Функция 13 |
XY импликация | |||||
|
Функция 14 |
отрицание на връзката |
F = (X Y) |
||||
|
Функция 15 |
константа 1 | |||||
КОМПЛЕКСНО ИЗКАЗВАНЕ
Ако няколко прости изявления се комбинират в едно с помощта на логически операции, тогава такова изявление се нарича сложно.
Винаги изхождаме от факта, че за никогопросто дефинирани изрази (известен ), независимо дали е вярно или невярно. отсложна форма твърдение и според таблиците на истинността на логическите операции, включени в него, винагиможе да се определи дали е вярно или невярно.
По правило получаваме истинската задача под формата на текст на естествен език. И преди да започнем да го решаваме, трябва да идентифицираме прости твърдения, отношения (връзки) между тях и да ги преведем на езика на формулите (формализирайте условието на проблема, определете формата). Нека да разгледаме примери за формализиране на сложни твърдения.
Определете формата на сложно твърдение
Пример 1. E = „Вашето пристигане не е нито необходимо, нито желателно“ Компоненти на твърдението: A = „Вашето пристигане е необходимо“; В = „Вашето пристигане е добре дошло“
Отговор: E= не(A) & не(B)
Пример 2. E = „Търсенето на врага продължи три часа, но нямаше резултати, скритият враг не се издаде.“ Компоненти на твърдението: A = „Търсенето на врага продължи три часа“ B = „Врагът беше открит (има резултат)“ C = „ Врагът се предаде.“Отговор:E= не(C) → A & не(B)
Пример 3. E = „Ако вчера беше облачно, значи днес слънцето грее ярко“ A = „Вчера беше облачно“; B = „Слънцето грее ярко днес“
Отговор: E = A → B
ПРИОРИТЕТ НА ЛОГИЧЕСКИТЕ ОПЕРАЦИИ
логиката като наука;
пропозиционална алгебра;
логически операции;
логически функции;
приоритет на логическите операции;
идентично верни и идентично неверни операции;
основни закони на алгебрата на логиката;
доказване на логически закони;
прости преобразуватели на информация;
домашна работа.
Изчисляването на стойностите на логическите изрази се извършва в определен ред, според техния приоритет:
- инверсия
- съчетание
- дизюнкция
- импликация и еквивалентност
Операциите с еднакъв приоритет се извършват отляво надясно. За промени в поръчкатасе използват действия скоби.
ПРИМЕР 1: A V (Б→ C) & D = не (A)
Ред на изпълнение:
Not(A) - инверсия
IN → C - импликация
(IN → C) & D - връзка
A V (Б → C) & D - дизюнкция
A V (Б → C) & D = не(A)-еквивалентност
Нека изградим таблица на истината за твърдението
E = (A V не(B)) → не(C)
Изявление E включва три променливи: A, B, C (n=3) и четири логически операции: инверсия B, инверсия C, дизюнкция, импликация.
Таблицата на истината ще се състои от 2 3 + 2 (заглавие) = 8 +2 = 10 реда и 3 + 4 = 7 колони
|
A v не (B)→не (C) |
||||||
ЕДНАКО ВЕРНИ И ЕДНАКО НЕВЕРНИ ТВЪРДЕНИЯ
логиката като наука;
пропозиционална алгебра;
логически операции;
логически функции;
приоритет на логическите операции;
идентично верни и идентично неверни операции;
основни закони на алгебрата на логиката;
доказване на логически закони;
прости преобразуватели на информация;
домашна работа.
Ако сложно твърдение е вярно за всички стойности на променливите, включени в него, тогава такова твърдение се нарича ИДЕНТИЧНО ВЯРНО или тавтология (обозначава се с константата 1).
НАПРИМЕР твърдението: "Демократ е човек, който изповядва демократични убеждения"- винаги е вярно, тоест е тавтология.
Всички математически, физически и други закони са тавтологии. Например: (a+b) 2 = a 2 + 2ab + b 2
Прогнозата за времето за утре може да бъде например така: — Ще вали или няма да вали.Такава прогноза винаги ще бъде вярна, въпреки че е малко вероятно да удовлетвори някого. Математическата му нотация:
A V not(A) = 1
(според закона за изключената среда, или предложението, или неговото отрицание трябва винаги да е вярно).
Можете да проверите дали сложно твърдение е идентично вярно, като използвате таблица на истината.
Ако сложно твърдение е невярно за всички стойности на променливите, включени в него, тогава такова твърдение се нарича ИДЕНТИЧНО НЕВЯРНО (означено с константата 0).
НАПРИМЕР твърдението: „Днес е сряда и това е вторият ден от седмицата“ е също толкова невярно. Следното твърдение е еднакво невярно: „Компютърът е включен и компютърът не е включен (изключен).“ Математическата му нотация е:
A & not(A) = 0
(според закона на противоречието: твърдение и неговото отрицание не могат да бъдат истинни едновременно.)
Ако значенията на сложните твърдения съвпадат за всички възможни стойности на променливите, включени в тях, тогава такива твърдения се наричат ЕКВИВАЛЕНТНИ, ИДЕНТИЧНИ, ЕКВИВАЛЕНТНИ
Опростяванесложни твърдения са замянаизявления до еквиваленттой се основава на законите на пропозиционалната алгебра
ОСНОВНИ ЗАКОНИ (РАВЕНСТВА) НА ЛОГИЧЕСКАТА АЛГЕБРА
логиката като наука;
пропозиционална алгебра;
логически операции;
логически функции;
приоритет на логическите операции;
идентично верни и идентично неверни операции;
основни закони на алгебрата на логиката;
доказване на логически закони;
прости преобразуватели на информация;
домашна работа.
Когато решавате логически задачи, често се налага да опростявате формули. Опростяването на формулите в булевата алгебра се извършва на базата на еквивалентни трансформации, базирани на основни закони.
Законите на пропозиционалната логика са изрази, които винаги съответстват на вярно твърдение, без значение какви замествания на стойности правим вместо променливи. В пропозиционалната алгебра логическите закони се изразяват под формата на формули.
1.1. Закон за идентичността:
Всяка мисъл е идентична на себе си, тоест „А е А“, където А е всяко твърдение.




