Метод динамического программирования применяется для решения. Решение задач динамического программирования. Два решения с различными состояниями

Программирование

Для выбора оптимального решения при выполнении задач программирования иногда требуется перебирать большое количество комбинаций данных, что нагружает память персонального компьютера. К таким методам относится, например, метод программирования «разделяй и властвуй». В данном случае алгоритмом предусмотрено разделение задачи на отдельные мелкие подзадачи. Такой метод применяется только в тех случаях, когда мелкие подзадачи независимы между собой. Для того чтобы избежать выполнения лишней работы в том случае, если подзадачи взаимозависимы, используется метод динамического программирования, предложенный американцем Р.Беллманом в 50-х годах.

Важную часть данных проблем можно решить с помощью динамического программирования. Возможность решать проблемы такого типа значительно повысит ваши навыки. Статья основана на примерах, потому что исходную теорию очень трудно понять. Примечание. Если вам скучно читать один раздел, и вы уже знаете, что обсуждается в нем, пропустите его и перейдите к следующему.

Что такое динамическое программирование, как его можно описать? Подрешение проблемы строится из ранее найденных. Прежде всего нам нужно найти состояние, для которого найдено оптимальное решение, и с помощью которого мы можем найти оптимальное решение для следующего состояния.

Суть метода

Динамическое программирование заключается в определении оптимального решения n-мерной задачи, разделяя ее n отдельных этапов. Каждый из них является подзадачей по отношению к одной переменной.

Основным преимуществом такого подхода можно считать то, что разработчики занимаются одномерными оптимизационными задачами подзадач вместо n-мерной задачи, а решение главной задачи собирается «снизу вверх».

Что означает «государство»? Это способ описать ситуацию, суб-решение проблемы. Прежде всего отметим, что для состояния 0 мы нашли решение с минимальным числом 0 монет. Во-первых, мы отмечаем, что мы еще не нашли решения для этого. Тогда мы видим, что только монета 1 меньше или равна текущей сумме. Поскольку мы добавляем одну монету к этому решению, у нас будет решение с 1 монетой для суммы. Это единственное решение, которое все еще найдено для этой суммы. Затем переходим к следующему состоянию - сумме 2.

В задачах линейного и нелинейного программирования, рассмотренных в предыдущих главах, экономический процесс считался статическим, т.е. не зависящим от времени, поэтому оптимальное решение находилось только на один этап планирования. Такие задачи получили название одноэтапных или одношаговых

Мы снова видим, что единственная монета, которая меньше или равна этой сумме, является первой монетой, имеющей значение. Эта монета 1 плюс первая монета суммируется до 2 и, таким образом, составляет сумму 2 с помощью всего 2 монет. Это лучшее и единственное решение для суммы. Теперь у нас есть 2 монеты, которые должны быть проанализированы - первая и вторая, имеющие значения 1 и существует решение для суммы 2, и поэтому мы можем построить из нее решение для суммы 3 из добавив к ней первую монету.

Целесообразно применять динамическое программирование в тех случаях, когда подзадачи взаимосвязаны, т.е. имеют общие модули. Алгоритмом предусмотрено решение каждой из подзадач один раз, и сохранение ответов выполняется в специальной таблице. Это дает возможность не вычислять ответ заново при встрече с аналогичной подзадачей.

Поскольку лучшее решение для суммы 2, которое мы нашли, имеет 2 монеты, новое решение для суммы 3 будет иметь 3 монеты. Теперь давайте возьмем вторую монету со значением, равным сумме, для которой эта монета должна быть добавлена, чтобы сделать 3, мы знаем, что сумма 0 состоит из 0 монет. Таким образом, мы можем сделать сумму 3 только с одной монетой. Мы видим, что это лучше, чем предыдущее найденное решение для суммы 3, состоящее из 3 монет.

Геометрическая интерпретация задачи динамического программирования

Мы обновляем его и отмечаем, что он имеет только 1 монету. То же самое мы делаем для суммы 4 и получаем решение из 2 монет - 1. Вот решения, найденные для всех сумм. В результате мы нашли решение из 3 монет, которые суммируются до. Кроме того, отслеживая данные о том, как мы получили определенную сумму из предыдущей, мы можем найти, какие монеты использовались при ее создании. Например: к сумме 11 мы получили добавление монеты со значением 1 к сумме.

Задача динамического программирования оптимизации. Автором этого метода Р. Беллманом был сформулирован принцип оптимальности: каким бы ни являлось начальное состояние на каждом из шагов и решение, определенное на этом шаге, все следующие выбираются оптимальными по отношению к тому состоянию, которое принимает система в конце шага.

В этом случае состояния не вычисляются последовательно. Рассмотрим проблему выше. Начните с решения 0 монет для суммы. Теперь давайте попробуем добавить первую монету ко всем уже найденным суммам. Затем мы делаем то же самое для второй монеты, третьей монеты и т.д. для остальных. Например, мы сначала добавляем монету 1 сумме 0 и получаем сумму. После обработки первой монеты возьмите монету 2 и последовательно попытайтесь добавить ее к каждой из уже найденных сумм. Добавив его в 0, вы получите сумму 3, состоящую из 1 монеты.

После добавления той же монеты к сумме 1 мы получим сумму 4, состоящую из 2 монет. То же самое делается для следующих сумм - каждый раз, когда найдено лучшее решение, результаты обновляются. К этому моменту обсуждались очень простые примеры. Теперь давайте посмотрим, как найти способ перехода из одного состояния в другое, для более сложных задач. Для этого мы введем новый термин, называемый рекуррентным соотношением, который связывает более низкое и большее состояние.

Метод усовершенствует выполнение задач, решаемых с помощью перебора вариантов или рекурсий.

Построение алгоритма задачи

Динамическое программирование предполагает построение такого алгоритма задач, при котором задача так разбивается на две или больше подзадач, чтобы ее решение складывалось из оптимального решения всех подзадач, входящих в нее. Далее возникает необходимость в написании рекуррентного соотношения и вычислении оптимального значения параметра для задачи в целом.

Этап II. Безусловная оптимизация

Найдите длину самой длинной неубывающей последовательности. Как описано выше, мы должны сначала найти, как определить «состояние», которое представляет собой под-проблему, и поэтому мы должны найти для нее решение. Обратите внимание, что в большинстве случаев состояния полагаются на более низкие состояния и не зависят от больших состояний.

Это состояние содержит только данные о длине этой последовательности. Подсказка. На каждом шаге среди вершин, которые еще не были проверены и для которых найден путь из вершины 1, возьмите тот, который имеет самый короткий путь, от вершины 1 к нему, но все же найден.

Иногда на 3-м шаге нужно дополнительно запоминать некоторую вспомогательную информацию о ходе выполнения каждой подзадачи. Это называется обратным ходом.

Применение метода

Динамическое программирование применяется при наличии двух характерных признаков:

оптимальность для подзадач;
наличие в задаче перекрывающихся подзадач.

Решая оптимизационную задачу методом динамического программирования, сначала необходимо описать структуру решения. Задача обладает оптимальностью, если решение задачи складывается из оптимальных решений ее подзадач. В этом случае целесообразно использовать динамическое программирование.

Динамическое программирование. Основные понятия

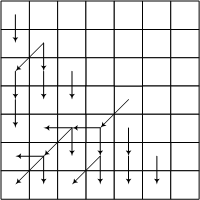
Попытайтесь решить следующие проблемы из капризов. Вы начинаете с верхнего левого угла. На каждом шагу вы можете спуститься или повернуть по одной ячейке. Найдите максимальное количество яблок, которые вы можете собрать. Прежде всего, мы должны найти состояние. Первое, что нужно заметить, - это то, что мы можем найти не более двух способов - влево и сверху. Таким образом, чтобы найти лучшее решение для этой ячейки, мы должны были найти наилучшие решения для всех ячеек, из которых мы можем попасть в текущую ячейку.

Второе свойство задачи, существенное при данном методе, - небольшое число подзадач. Рекурсивное решение задачи использует одни и те же перекрывающиеся подзадачи, количество которых зависит от размера исходной информации. Ответ хранится в специальной таблице, программа экономит время, пользуясь этими данными.

Особенно эффективно применение динамического программирования тогда, когда по существу задачи нужно принимать решения поэтапно. Например, рассмотрим простой пример задачи замены и ремонта оборудования. Допустим, на литейной машине завода по изготовлению шин делают одновременно шины в двух разных формах. В том случае, если одна из форм выходит из строя, приходится машину разбирать. Понятно, что иногда выгоднее заменить и вторую форму для того, чтобы не разбирать машину на случай, если и эта форма окажется неработоспособной на следующем этапе. Тем более, бывает проще заменить обе работающие формы до того, как они начнут выходить из строя. Метод динамического программирования определяет наилучшую стратегию в вопросе о замене таких форм, учитывая все факторы: выгоду от продолжения эксплуатации форм, потери от простоя машины, стоимость забракованных шин и другое.

Сверху можно легко получить рекуррентное соотношение. Вот несколько проблем, начиная с кастета, для практики. Хорошим примером может служить следующая проблема. Если у вас недостаточно денег, вы не можете пройти через эту вершину. Если существует более одного пути с одинаковой длиной, выведите самый дешевый. Пусть это состояние будет найдено. Следующие проблемы потребуют хороших наблюдений, чтобы уменьшить их до динамического решения.

В каждой клетке есть несколько яблок. Вы начинаете с верхнего левого угла матрицы. Вы можете спуститься или спуститься по одной ячейке. Вам нужно прибыть в нижний правый угол. Затем вам нужно вернуться в верхнюю левую ячейку, пройдя каждый шаг на одну ячейку слева или вверх. Прибыв в эту верхнюю левую ячейку, вам нужно снова вернуться в нижнюю правую клетку.

Здравствуй, Хабрахабр. В настоящий момент я работаю над учебным пособием по олимпиадному программированию, один из параграфов которого посвящен динамическому программированию. Ниже приведена выдержка из данного параграфа. Пытаясь объяснить данную тему как можно проще, я постарался сложные моменты сопроводить иллюстрациями. Мне интересно ваше мнение о том, насколько понятным получился данный материал. Также буду рад советам, какие еще задачи стоит включить в данный раздел.

Когда вы проходите через камеру, вы собираете все яблоки, оставленные там. Прежде всего заметим, что эта проблема похожа на классическую, в которой вам нужно идти только один раз из верхней левой клетки в нижнюю правую, собирая максимально возможное количество яблок. Было бы лучше попытаться свести проблему к этому. Первое наблюдение заключается в том, что мы можем рассматривать второй путь как путь, идущий от верхней левой до нижней правой ячейки. Это не имеет никакого значения, потому что путь, пройденный снизу вверх, может передаваться сверху вниз только в обратном порядке.

Во многих олимпиадных задачах по программированию решение с помощью рекурсии или полного перебора требует выполнения очень большого числа операций. Попытка решить такие задачи, например, полным перебором, приводит к превышению времени выполнения.

Однако среди переборных и некоторых других задач можно выделить класс задач, обладающих одним хорошим свойством: имея решения некоторых подзадач (например, для меньшего числа n ), можно практически без перебора найти решение исходной задачи.

Таким образом мы получаем три пути, идущих сверху вниз. Это как-то уменьшает сложность проблемы. Мы можем рассматривать эти 3 пути как левые, средние и правые. Когда 2 пути пересекаются. Мы можем рассматривать их как на следующем рисунке, не влияя на результат.

Одномерное динамическое программирование

Таким образом, мы получим 3 пути, которые мы можем рассматривать как один левый, один средний, другой - правый. Более того, мы можем видеть, что для получения оптимальных результатов они не должны пересекаться. Теперь нам нужно найти только путь перехода от одной строки к следующей.

Такие задачи решают методом динамического программирования, а под самим динамическим программированием понимают сведение задачи к подзадачам.

Последовательности

Классической задачей на последовательности является следующая.

Последовательность Фибоначчи F n задается формулами: F 1 = 1, F 2 = 1,
F n = F n - 1 + F n - 2 при n > 1. Необходимо найти F n по номеру n .

Таким образом, мы опускаемся на каждом шагу. После того, как мы сделали такой шаг, мы должны учитывать, что пути могут перемещаться вправо вправо. Чтобы сохранить пути из пересечения, мы должны сначала рассмотреть переход справа от левого пути, после этого из среднего пути, а затем по правильному пути. Когда вы прочитали описание проблемы и начали ее решать, сначала посмотрите на ее ограничения. В этом случае попробуйте выяснить, существуют ли такие состояния, с помощью которых могут быть найдены следующие состояния.

Планирование производственной линии

Обнаружив это, подумайте о том, как перейти из одного состояния в другое. Нужна специфика о процессе или правилах? Динамический подход к программированию аналогичен разграничению и покорению при разбивке проблемы на более мелкие и все же меньшие возможные проблемы. Но в отличие от этого, разделять и побеждать, эти подзадачи не решаются самостоятельно. Скорее, результаты этих меньших под-проблем запоминаются и используются для аналогичных или перекрывающихся под-проблем.

Один из способов решения, который может показаться логичным и эффективным, — решение с помощью рекурсии:

Int F(int n) { if (n < 2) return 1; else return F(n - 1) + F(n - 2); }
Используя такую функцию, мы будем решать задачу «с конца» — будем шаг за шагом уменьшать n , пока не дойдем до известных значений.

Но как можно заметить, такая, казалось бы, простая программа уже при n = 40 работает заметно долго. Это связано с тем, что одни и те же промежуточные данные вычисляются по несколько раз — число операций нарастает с той же скоростью, с какой растут числа Фибоначчи — экспоненциально.

Динамическое программирование используется там, где у нас есть проблемы, которые можно разделить на аналогичные подзадачи, чтобы их результаты можно было повторно использовать. В основном эти алгоритмы используются для оптимизации. Прежде чем решать внутреннюю проблему, динамический алгоритм попытается проанализировать результаты ранее разрешенных подзадач. Решения подзадач объединяются для достижения наилучшего решения.

Оптимальное решение может быть достигнуто с помощью оптимального решения меньших подзадач.

Проблема должна быть разделена на более мелкую дублирующую суб-проблему.
Динамические алгоритмы используют запоминание.

В отличие от жадных алгоритмов, в которых устранена локальная оптимизация, динамические алгоритмы мотивированы на общую оптимизацию проблемы.

Один из выходов из данной ситуации — сохранение уже найденных промежуточных результатов с целью их повторного использования:

Int F(int n) { if (A[n] != -1) return A[n]; if (n < 2) return 1; else { A[n] = F(n - 1) + F(n - 2); return A[n]; } }
Приведенное решение является корректным и эффективным. Но для данной задачи применимо и более простое решение:

F = 1; F = 1; for (i = 2; i < n; i++) F[i] = F + F;
Такое решение можно назвать решением «с начала» — мы первым делом заполняем известные значения, затем находим первое неизвестное значение (F 3), потом следующее и т.д., пока не дойдем до нужного.

В отличие от алгоритмов разделения и покорения, когда решения объединяются для достижения общего решения, динамические алгоритмы используют вывод меньшей суб-проблемы, а затем пытаются оптимизировать большую под-проблему. Динамические алгоритмы используют запоминание для запоминания результатов уже разрешенных подзадач.

Следующие компьютерные проблемы могут быть решены с использованием подхода динамического программирования -. Ряд чисел Фибоначчи Задача Рюкзак Башня Ханоя Все пары кратчайшего пути Флойда-Варшалла Самый короткий путь по Дийкстре Планирование проекта. Динамическое программирование может использоваться как сверху вниз, так и снизу вверх.

Именно такое решение и является классическим для динамического программирования: мы сначала решили все подзадачи (нашли все F i для i < n ), затем, зная решения подзадач, нашли ответ (F n = F n - 1 + F n - 2 , F n - 1 и F n - 2 уже найдены).

Одномерное динамическое программирование

Чтобы лучше понять суть динамического программирования, сначала более формально определим понятия задачи и подзадачи.

Пусть исходная задача заключается в нахождении некоторого числа T при исходных данных n 1 , n 2 , ..., n k . То есть мы можем говорить о функции T (n 1 , n 2 , ..., n k ), значение которой и есть необходимый нам ответ. Тогда подзадачами будем считать задачи
T (i 1 , i 2 , ..., i k ) при i 1 < n 1 , i 2 < n 2 , ..., i k < n k .

Это оптимизация вашего алгоритма, который сокращает время выполнения. Хотя алчный алгоритм обычно называют наивным, поскольку он может работать несколько раз по одному и тому же набору данных, динамическое программирование позволяет избежать этой ошибки путем более глубокого понимания частичных результатов, которые необходимо сохранить, чтобы помочь построить окончательное решение.

Простым примером является перемещение дерева или графика только через узлы, которые будут вносить вклад в решение, или помещая в таблицу решения, которые вы обнаружили до сих пор, чтобы вы могли избежать повторения одних и тех же узлов снова и снова. Взгляните на эту проблему, если мы определим функцию стоимости, рассказывающую нам, насколько далеки две строки, мы рассмотрим три естественных типа изменений.

Следующая задача одномерного динамического программирования встречается в различных вариациях.

При n < 32 полный перебор потребует нескольких секунд, а при n = 64 полный перебор не осуществим в принципе. Для решения задачи методом динамического программирования сведем исходную задачу к подзадачам.

При n = 1, n = 2 ответ очевиден. Допустим, что мы уже нашли K n - 1 , K n - 2 — число таких последовательностей длины n - 1 и n - 2.

Посмотрим, какой может быть последовательность длины n . Если последний ее символ равен 0, то первые n - 1 — любая правильная последовательность длины
n - 1 (не важно, заканчивается она нулем или единицей — следом идет 0). Таких последовательностей всего K n - 1 . Если последний символ равен 1, то предпоследний символ обязательно должен быть равен 0 (иначе будет две единицы подряд), а первые
n - 2 символа — любая правильная последовательность длины n - 2, число таких последовательностей равно K n - 2 .

Таким образом, K 1 = 2, K 2 = 3, K n = K n - 1 + K n - 2 при n > 2. То есть данная задача фактически сводится к нахождению чисел Фибоначчи.

Двумерное динамическое программирование

Классической задачей двумерного динамического программирования является задача о маршрутах на прямоугольном поле.
В разных формулировках необходимо посчитать число маршрутов или найти маршрут, который является лучшим в некотором смысле.

Приведем пару формулировок таких задач:

Задача 2. n *m клеток. Можно совершать шаги длиной в одну клетку вправо или вниз. Посчитать, сколькими способами можно попасть из левой верхней клетки в правую нижнюю.

Задача 3. Дано прямоугольное поле размером n *m клеток. Можно совершать шаги длиной в одну клетку вправо, вниз или по диагонали вправо-вниз. В каждой клетке записано некоторое натуральное число. Необходимо попасть из верхней левой клетки в правую нижнюю. Вес маршрута вычисляется как сумма чисел со всех посещенных клеток. Необходимо найти маршрут с минимальным весом.

Для всех таких задач характерным является то, что каждый отдельный маршрут не может пройти два или более раз по одной и той же клетке.

Рассмотрим более подробно задачу 2. В некоторую клетку с координатами (i ,j ) можно прийти только сверху или слева, то есть из клеток с координатами (i - 1, j ) и (i , j - 1):

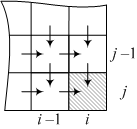
Таким образом, для клетки (i , j ) число маршрутов A[i][j] будет равно
A[j] + A[i], то есть задача сводится к двум подзадачам. В данной реализации используется два параметра — i и j — поэтому применительно к данной задаче мы говорим о двумерном динамическом программировании.

Теперь мы можем пройти последовательно по строкам (или по столбцам) массива A, находя число маршрутов для текущей клетки по приведенной выше формуле. Предварительно в A необходимо поместить число 1.

В задаче 3 в клетку с координатами (i , j ) мы можем попасть из клеток с координатами
(i - 1, j), (i , j - 1) и (i - 1, j - 1). Допустим, что для каждой из этих трех клеток мы уже нашли маршрут минимального веса, а сами веса поместили в W[j], W[i],
W. Чтобы найти минимальный вес для (i , j ), необходимо выбрать минимальный из весов W[j], W[i], W и прибавить к нему число, записанное в текущей клетке:

W[i][j] = min(W[j], W[i], W) + A[i][j];

Данная задача осложнена тем, что необходимо найти не только минимальный вес, но и сам маршрут. Поэтому в другой массив мы дополнительно для каждой клетки будем записывать, с какой стороны в нее надо попасть.

На следующем рисунке приведен пример исходных данных и одного из шагов алгоритма.

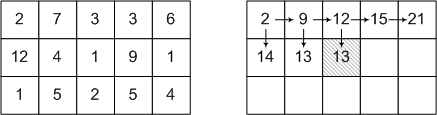
В каждую из уже пройденных клеток ведет ровно одна стрелка. Эта стрелка показывает, с какой стороны необходимо прийти в эту клетку, чтобы получить минимальный вес, записанный в клетке.

После прохождения всего массива необходимо будет проследить сам маршрут из последней клетки, следуя по стрелкам в обратную сторону.

Задачи на подпоследовательности

Рассмотрим задачу о возрастающей подпоследовательности.

Задача 4. Дана последовательность целых чисел. Необходимо найти ее самую длинную строго возрастающую подпоследовательность.

Начнем решать задачу с начала — будем искать ответ, начиная с первых членов данной последовательности. Для каждого номера i будем искать наибольшую возрастающую подпоследовательность, оканчивающуюся элементом в позиции i . Пусть исходная последовательность хранится в массиве A. В массиве L будем записывать длины максимальных подпоследовательностей, оканчивающихся текущим элементом. Пусть мы нашли все L[i] для 1 <= i <= k - 1. Теперь можно найти L[k] следующим образом. Просматриваем все элементы A[i] для 1 <= i < k - 1. Если
A[i] < A[k], то k -ый элемент может стать продолжением подпоследовательности, окончившейся элементом A[i]. Длина полученной подпоследовательности будет на 1 больше L[i]. Чтобы найти L[k], необходимо перебрать все i от 1 до k - 1:
L[k] = max(L[i]) + 1, где максимум берется по всем i таким, что A[i] < A[k] и
1 <= i < k .

Здесь максимум из пустого множества будем считать равным 0. В этом случае текущий элемент станет единственным в выбранной последовательности, а не будет продолжением одной из предыдущих. После заполнения массива L длина наибольшей возрастающей подпоследовательности будет равна максимальному элементу L.

Чтобы восстановить саму подпоследовательность, можно для каждого элемента также сохранять номер предыдущего выбранного элемента, например, в массив N.

Рассмотрим решение этой задачи на примере последовательности 2, 8, 5, 9, 12, 6. Поскольку до 2 нет ни одного элемента, то максимальная подпоследовательность содержит только один элемент — L = 1, а перед ним нет ни одного — N = 0. Далее,
2 < 8, поэтому 8 может стать продолжением последовательности с предыдущим элементом. Тогда L = 2, N = 1.

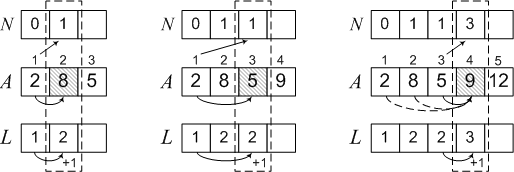
Меньше A = 5 только элемент A = 2, поэтому 5 может стать продолжением только одной подпоследовательности — той, которая содержит 2. Тогда
L = L + 1 = 2, N = 1, так как 2 стоит в позиции с номером 1. Аналогично выполняем еще три шага алгоритма и получаем окончательный результат.

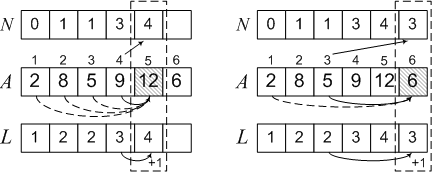
Теперь выбираем максимальный элемент в массиве L и по массиву N восстанавливаем саму подпоследовательность 2, 5, 9, 12.

Еще одной классической задачей динамического программирования является задача о палиндромах.

Задача 5. Дана строка из заглавных букв латинского алфавита. Необходимо найти длину наибольшего палиндрома, который можно получить вычеркиванием некоторых букв из данной строки.

Обозначим данную строку через S, а ее символы — через S[i], 1 <= i <= n . Будем рассматривать возможные подстроки данной строки с i -го по j -ый символ, обозначим их через S (i , j ). Длины максимальных палиндромов для подстрок будем записывать в квадратный массив L: L[i][j] — длина максимального палиндрома, который можно получить из подстроки S (i , j ).

Начнем решать задачу с самых простых подстрок. Для строки из одного символа (то есть подстроки вида S (i , i )) ответ очевиден — ничего вычеркивать не надо, такая строка будет палиндромом. Для строки из двух символов S (i , i + 1) возможны два варианта: если символы равны, то мы имеем палиндром, ничего вычеркивать не надо. Если же символы не равны, то вычеркиваем любой.

Пусть теперь нам дана подстрока S (i , j ). Если первый (S[i]) и последний (S[j]) символы подстроки не совпадают, то один из них точно нужно вычеркнуть. Тогда у нас останется подстрока S (i , j - 1) или S (i + 1, j ) — то есть мы сведем задачу к подзадаче: L[i][j] = max(L[i], L[j]). Если же первый и последний символы равны, то мы можем оставить оба, но необходимо знать решение задачи S (i + 1, j - 1):
L[i][j] = L + 2.

Рассмотрим решение на примере строки ABACCBA. Первым делом заполняем диагональ массива единицами, они будут соответствовать подстрокам S (i , i ) из одного символа. Затем начинаем рассматривать подстроки длины два. Во всех подстроках, кроме S (4, 5), символы различны, поэтому в соответствующие ячейки запишем 1, а в L — 2.

Получается, что мы будем заполнять массив по диагоналям, начиная с главной диагонали, ведущей из левого верхнего угла в правый нижний. Для подстрок длины 3 получаются следующие значения: в подстроке ABA первая и последняя буквы равны, поэтому
L = L + 2. В остальных подстроках первая и последняя буквы различны.

BAC: L = max(L, L) = 1.
ACC: L = max(L, L) = 2.
CCB: L = max(L, L) = 2.
CBA: L = max(L, L) = 1.

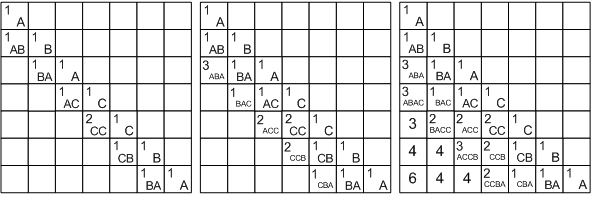
Если же в задаче необходимо вывести не длину, а сам палиндром, то дополнительно к массиву длин мы должны построить массив переходов — для каждой ячейки запомнить, какой из случаев был реализован (на рисунке для наглядности вместо числовых значений, кодирующих переходы, нарисованы соответствующие стрелки).